Dec 19, 2020

[CTF Writeup] X-MAS 2020 - Santa's ELF holomorphing machine

CTF: Xmas CTF 2020
Challenge: Santa’s ELF holomorphing machine Category: Programming
Points: 424

We have intercepted the blueprints and a memory dump for another of Santa's wicked contraptions. What is the old man hiding this time around?

Author: PinkiePie1189

Full code for my solution available here.

The linked document tells us that the machine works by taking each elf (complex number), and mapping it to somewhere else on the complex plane using a holomorphic function.

However it only stores either the real part u(x, y) or the imaginary part v(x, y) of each function f(x + yi) = u(x,y) + v(x,y)i, not both.

The attached file data.txt contains all the functions and points to map in the following format:

u = -3 * x + 95 * y; z = -0.12652202789462033 + 0.006530883329643569 * i
v = -65 * x + 5 * y; z = -0.16588235294117648 + 0.04352941176470588 * i
<hundreds more>

Since holomorphic functions are unusually well behaved, it is actually possible in general to compute u(x,y) given v(x,y) and vice-versa.

I noticed that all the functions in this challenge were linear functions of the form ax + by, so with some (literally) back-of-the-envelope calculations using the Cauchy-Riemann Equations, we can quickly derive the solutions for this specific case:

Back of the envelope calculations

Back of the envelope calculations

Using these derivations, I wrote a python script to take each function/point pair, compute the full holomorphic function and map the point accordingly.

class Case():
    def __init__(self, var, x, y, zx, zy):
        self.var = var
        self.x = x
        self.y = y
        self.zx = zx
        self.zy = zy

    def __str__(self):
        return f"{self.var} = {self.x} * x + {self.y} * y; z = {self.zx} + {self.zy} * i"

    def solve(self):
        if self.var == "u":
            return self.solve_u()
        else:
            return self.solve_v()

    def solve_u(self):
        a, b = self.x, self.y
        x, y = self.zx, self.zy
        return (a * x + b * y, a * y - b * x)

    def solve_v(self):
        a, b = self.x, self.y
        x, y = self.zx, self.zy
        return (b * x - a * y, a * x + b * y)

I noticed that the results were all integer coordinates, so assumed they would create an image. I then used the python library Pillow to generate an image from these points and get the flag:

Flag

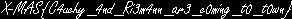
Flag